We begin with the 2x2 identity matrix, which has the property:
$$\begin{pmatrix}1 & 0\\\ 0 & 1\end{pmatrix} \begin{pmatrix}a \\\ b\end{pmatrix} = \begin{pmatrix}a \\\ b\end{pmatrix}$$Let's "unfurl" the 2x2 identity matrix into a 4x1 vector.
$$\begin{pmatrix}1 & 0\\\ 0 & 1\end{pmatrix} \Rightarrow \begin{pmatrix}1 \\ 0 \\ 0 \\ 1\end{pmatrix}$$How can we interpret this?
Suppose we have two qubits A and B.
$$ A = a\mid\uparrow\rangle + b\mid\downarrow\rangle \\ B = c\mid\uparrow\rangle + d\mid\downarrow\rangle \\ $$where $\mid\uparrow\rangle = \begin{pmatrix}1 \\\ 0\end{pmatrix} $, $\mid\downarrow\rangle = \begin{pmatrix}0 \\\ 1\end{pmatrix} $, and $a, b, c, d \in \mathbb{C}$.
Their tensor product $ A \otimes B $ lives in:
$$ \alpha\mid\uparrow\uparrow\rangle + \beta\mid\uparrow\downarrow\rangle + \gamma\mid\downarrow\uparrow\rangle + \delta\mid\downarrow\downarrow\rangle $$We can therefore interpret $ \begin{pmatrix}1 \\ 0 \\ 0 \\ 1\end{pmatrix} $ as: $$A,B$$ $$ \begin{matrix} \mid\uparrow\uparrow\rangle \\ \mid\uparrow\downarrow\rangle \\ \mid\downarrow\uparrow\rangle \\ \mid\downarrow\downarrow\rangle \end{matrix} \begin{pmatrix} 1 \\ 0 \\ 0 \\ 1\end{pmatrix} $$
In other words, as: $\mid\uparrow\uparrow\rangle \ + \mid\downarrow\downarrow\rangle$, one of the four maximally entangled states of two qubits. There's an equal probability for both qubits to be in the up state or both qubits to be in the down state: but if one is up, then the other must be up, and vice versa.
A word on "bra/ket" formalism:
$$ \mid ket \rangle \ \Rightarrow \begin{pmatrix}a \\ b \\ c \\ \vdots \end{pmatrix} $$$ \langle bra \mid \ \Rightarrow \begin{pmatrix}a^{*} & b^{*} & c^{*} & \dots \end{pmatrix} $, where $a^{*}$ is complex conjugation: $x+iy \to x-iy$.
The inner product: $\langle bra \mid ket \rangle \Rightarrow \begin{pmatrix}a^{*} & b^{*} & c^{*} & \dots \end{pmatrix} \begin{pmatrix}a \\ b \\ c \\ \vdots \end{pmatrix} \Rightarrow a^{*}a \ + b^{*}b \ + c^{*}c \ + \dots $
The outer product: $\mid ket \rangle \langle bra \mid \ \Rightarrow \begin{pmatrix}a \\ b \\ c \\ \vdots \end{pmatrix} \begin{pmatrix}a^{*} & b^{*} & c^{*} & \dots \end{pmatrix} \Rightarrow \begin{pmatrix} aa^{*} & ab^{*} & ac^{*} & \dots \\ ba^{*} & bb^{*} & bc^{*} & \dots \\ ca^{*} & cb^{*} & cc^{*} & \dots \\ \vdots & \vdots & \vdots & \vdots \end{pmatrix} $
$$\mid\uparrow\uparrow\rangle \Rightarrow \begin{pmatrix}1 \\\ 0\end{pmatrix} \otimes \begin{pmatrix}1 \\\ 0\end{pmatrix} \Rightarrow \begin{pmatrix}1 \\\ 0 \\\ 0 \\\ 0\end{pmatrix}$$Expectation value of operator O: $\langle bra\mid O \mid ket \rangle $
Projectors onto up state: $ \mid \uparrow \rangle \langle \uparrow \mid \ \Rightarrow \begin{pmatrix}1 & 0 \\\ 0 & 0\end{pmatrix}$ and down state: $ \mid \downarrow \rangle \langle \downarrow \mid \ \Rightarrow \begin{pmatrix}0 & 0 \\\ 0 & 1\end{pmatrix}$
Probability: $\langle bra \mid projector \mid ket \rangle $.
If we have two qubits, A on the left and B on the right, we can consider operators that act only on the left or the right.
$$O_{L} = O \otimes I \Rightarrow \begin{pmatrix}a & b \\\ c & d\end{pmatrix} \otimes \begin{pmatrix}1 & 0 \\\ 0 & 1\end{pmatrix} \Rightarrow \begin{pmatrix}a & 0 & b & 0 \\\ 0 & a & 0 & b \\ c & 0 & d & 0 \\ 0 & c & 0 & d\end{pmatrix}\\ \\$$$$O_{R} = I \otimes O \Rightarrow \begin{pmatrix}1 & 0 \\\ 0 & 1\end{pmatrix} \otimes \begin{pmatrix}a & b \\\ c & d\end{pmatrix} \Rightarrow \begin{pmatrix}a & b & 0 & 0 \\\ c & d & 0 & 0 \\ 0 & 0 & a & b \\ 0 & 0 & c & d\end{pmatrix}$$For example, let's see what happens if we act with an $\uparrow$ projector on the left half of our maximally entangled state:
$$ (\mid \uparrow \rangle \langle \uparrow \mid \otimes I)(\mid\uparrow\uparrow\rangle \ + \mid\downarrow\downarrow\rangle) \Rightarrow \big( \begin{pmatrix}1 & 0 \\\ 0 & 0\end{pmatrix} \otimes \begin{pmatrix}1 & 0 \\\ 0 & 1\end{pmatrix} \big) \big( \begin{pmatrix}1 \\ 0 \\ 0 \\ 0\end{pmatrix} + \begin{pmatrix}0 \\ 0 \\ 0 \\ 1\end{pmatrix}\big) \Rightarrow \begin{pmatrix}1 & 0 & 0 & 0 \\\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0\end{pmatrix}\begin{pmatrix}1 \\ 0 \\ 0 \\ 1\end{pmatrix} \Rightarrow \begin{pmatrix}1 \\ 0 \\ 0 \\ 0\end{pmatrix} = \ \mid\uparrow\uparrow\rangle $$And with the $\downarrow$ projector:
$$ (\mid \downarrow \rangle \langle \downarrow \mid \otimes I)(\mid\uparrow\uparrow\rangle \ + \mid\downarrow\downarrow\rangle) \Rightarrow \big( \begin{pmatrix}0 & 0 \\\ 0 & 1\end{pmatrix} \otimes \begin{pmatrix}1 & 0 \\\ 0 & 1\end{pmatrix} \big) \big( \begin{pmatrix}1 \\ 0 \\ 0 \\ 0\end{pmatrix} + \begin{pmatrix}0 \\ 0 \\ 0 \\ 1\end{pmatrix}\big) \Rightarrow \begin{pmatrix}0 & 0 & 0 & 0 \\\ 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1\end{pmatrix}\begin{pmatrix}1 \\ 0 \\ 0 \\ 1\end{pmatrix} \Rightarrow \begin{pmatrix}0 \\ 0 \\ 0 \\ 1\end{pmatrix} = \ \mid\downarrow\downarrow\rangle $$And symmetrically with the projectors on the right side:
$$ (I \otimes \mid \uparrow \rangle \langle \uparrow \mid)(\mid\uparrow\uparrow\rangle \ + \mid\downarrow\downarrow\rangle) \Rightarrow \big( \begin{pmatrix}1 & 0 \\\ 0 & 1\end{pmatrix} \otimes \begin{pmatrix}1 & 0 \\\ 0 & 0\end{pmatrix} \big) \begin{pmatrix}1 \\ 0 \\ 0 \\ 1\end{pmatrix} \Rightarrow \begin{pmatrix}1 & 0 & 0 & 0 \\\ 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0\end{pmatrix}\begin{pmatrix}1 \\ 0 \\ 0 \\ 1\end{pmatrix} \Rightarrow \begin{pmatrix}1 \\ 0 \\ 0 \\ 0\end{pmatrix} = \ \mid\uparrow\uparrow\rangle $$$$ (I \otimes \mid \downarrow \rangle \langle \downarrow \mid)(\mid\uparrow\uparrow\rangle \ + \mid\downarrow\downarrow\rangle) \Rightarrow \big( \begin{pmatrix}1 & 0 \\\ 0 & 1\end{pmatrix} \otimes \begin{pmatrix}0 & 0 \\\ 0 & 1\end{pmatrix} \big) \begin{pmatrix}1 \\ 0 \\ 0 \\ 1\end{pmatrix} \Rightarrow \begin{pmatrix}0 & 0 & 0 & 0 \\\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1\end{pmatrix}\begin{pmatrix}1 \\ 0 \\ 0 \\ 1\end{pmatrix} \Rightarrow \begin{pmatrix}0 \\ 0 \\ 0 \\ 1\end{pmatrix} = \ \mid\downarrow\downarrow\rangle $$Meanwhile, the probability of getting $\uparrow$ on the left side. Note that to get the right answer we have to normalize our state so that probabilities sum to 1: $ \frac{1}{\sqrt{2}} (\mid\uparrow\uparrow\rangle \ + \mid\downarrow\downarrow\rangle) $.
$$ \frac{1}{\sqrt{2}}(\langle \uparrow\uparrow\mid + \ \langle\downarrow\downarrow\mid)(\mid \uparrow \rangle \langle \uparrow \mid \otimes I)\frac{1}{\sqrt{2}}(\mid\uparrow\uparrow\rangle \ + \mid\downarrow\downarrow\rangle) \Rightarrow \begin{pmatrix}\frac{1}{\sqrt{2}} & 0 & 0 & \frac{1}{\sqrt{2}}\end{pmatrix} \begin{pmatrix}1 & 0 & 0 & 0 \\\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0\end{pmatrix}\begin{pmatrix}\frac{1}{\sqrt{2}} \\ 0 \\ 0 \\ \frac{1}{\sqrt{2}}\end{pmatrix} \Rightarrow \frac{1}{2} $$The same is true on the up projector on the right side, and for the down projectors on the left and right.
Let's consider the difference between a general 2x2 operator $ O = \begin{pmatrix}a & b \\ c & d\end{pmatrix} $ acting on the left vs the right on our maximally entangled state, which we should give a name: $\mid \phi^{+} \rangle$.
$$O_{L}\mid \phi^{+} \rangle = \big( \begin{pmatrix}a & b \\\ c & d\end{pmatrix} \otimes \begin{pmatrix}1 & 0 \\\ 0 & 1\end{pmatrix} \big) \begin{pmatrix}1 \\ 0 \\ 0 \\ 1\end{pmatrix} \Rightarrow \begin{pmatrix}a & 0 & b & 0 \\\ 0 & a & 0 & b \\ c & 0 & d & 0 \\ 0 & c & 0 & d\end{pmatrix}\begin{pmatrix}1 \\ 0 \\ 0 \\ 1\end{pmatrix} \Rightarrow \begin{pmatrix}a \\ b \\ c \\ d\end{pmatrix}$$We get the 2x2 operator O unfurled as a 4x1 vector!
What about on the right?
$$O_{R}\mid \phi^{+} \rangle = \big( \begin{pmatrix}1 & 0 \\\ 0 & 1\end{pmatrix} \otimes \begin{pmatrix}a & b \\\ c & d\end{pmatrix} \big) \begin{pmatrix}1 \\ 0 \\ 0 \\ 1\end{pmatrix} \Rightarrow \begin{pmatrix}a & b & 0 & 0 \\\ c & d & 0 & 0 \\ 0 & 0 & a & b \\ 0 & 0 & c & d\end{pmatrix}\begin{pmatrix}1 \\ 0 \\ 0 \\ 1\end{pmatrix} \Rightarrow \begin{pmatrix}a \\ c \\ b \\ d\end{pmatrix}$$Let's define $O^{T}$ to be the transpose of O. In other words, interchange rows and columns.
$$O^{T} = \begin{pmatrix}a & c \\\ b & d\end{pmatrix} $$We observe that:
$$O_{R}^{T}\mid \phi^{+} \rangle = \big( \begin{pmatrix}1 & 0 \\\ 0 & 1\end{pmatrix} \otimes \begin{pmatrix}a & c \\\ b & d\end{pmatrix} \big) \begin{pmatrix}1 \\ 0 \\ 0 \\ 1\end{pmatrix} \Rightarrow \begin{pmatrix}a & c & 0 & 0 \\\ b & d & 0 & 0 \\ 0 & 0 & a & c \\ 0 & 0 & b & d\end{pmatrix}\begin{pmatrix}1 \\ 0 \\ 0 \\ 1\end{pmatrix} \Rightarrow \begin{pmatrix}a \\ b \\ c \\ d\end{pmatrix}$$And conclude:
$$ O_{L}\mid \phi^{+} \rangle = O_{R}^{T}\mid \phi^{+} \rangle$$Introducing the diagram language.
$\mid\uparrow\uparrow\rangle\ + \mid\downarrow\downarrow\rangle \ \Rightarrow \cup $
$\langle\uparrow\uparrow\mid + \langle\downarrow\downarrow\mid \ \Rightarrow \cap $
$ \begin{pmatrix}1 & 0 \\\ 0 & 1\end{pmatrix} \Rightarrow \ \mid $
$ \begin{matrix} \fbox{A} & \fbox{B} \end{matrix} \Rightarrow A \otimes B $
$ \begin{matrix} \fbox{A} \\ \fbox{B} \end{matrix} \Rightarrow A * B $
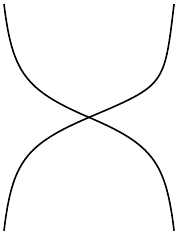 $ \Rightarrow \begin{pmatrix}1 & 0 & 0 & 0\\\ 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 &1\end{pmatrix} $
$ \Rightarrow \begin{pmatrix}1 & 0 & 0 & 0\\\ 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 &1\end{pmatrix} $
The yanking equation.
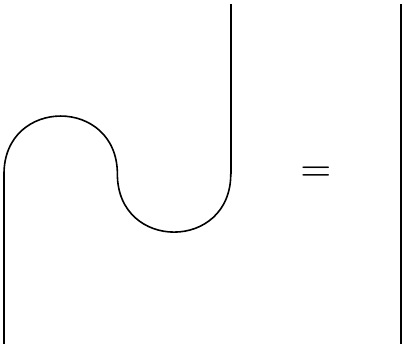
We can interpret this by slicing the diagram horizontally, and moving from bottom to top.
So in the first layer, we have a wire next to a cup: $I \otimes \mid \phi^{+} \rangle$.
In the second layer, we have cap next to a wire: $ \langle \phi^{+} \mid \otimes I $.
The yanking equation says that $ \big( \langle \phi^{+} \mid \otimes I \big) \big( I \otimes \mid \phi^{+} \rangle \big) = I $.
Let's check:
$$ \big( \begin{pmatrix}1 & 0 & 0 & 1\end{pmatrix} \otimes \begin{pmatrix}1 & 0 \\\ 0 & 1\end{pmatrix} \big) \big( \begin{pmatrix}1 & 0 \\\ 0 & 1\end{pmatrix} \otimes \begin{pmatrix}1 \\ 0 \\ 0 \\ 1\end{pmatrix} \big) = \begin{pmatrix}1 & 0 \\\ 0 & 1\end{pmatrix} $$$$ \begin{pmatrix}1 & 0 & 0 & 0 & 0 & 0 & 1 & 0\\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 1\end{pmatrix} \begin{pmatrix}1 & 0 \\ 0 & 0 \\ 0 & 0 \\ 1 & 0 \\ 0 & 1 \\ 0 & 0 \\ 0 & 0 \\ 0 & 1\end{pmatrix} = \begin{pmatrix}1 & 0 \\\ 0 & 1\end{pmatrix} $$Indeed for some state A entering the wire: $ \big( \langle \phi^{+} \mid \otimes I \big) \big( A \otimes \mid \phi^{+} \rangle \big) = A $.
$$ \big( \begin{pmatrix}1 & 0 & 0 & 1\end{pmatrix} \otimes \begin{pmatrix}1 & 0 \\\ 0 & 1\end{pmatrix} \big) \big( \begin{pmatrix}a & b \\\ c & d\end{pmatrix} \otimes \begin{pmatrix}1 \\ 0 \\ 0 \\ 1\end{pmatrix} \big) = \begin{pmatrix}a & b \\\ c & d\end{pmatrix} $$$$ \begin{pmatrix}1 & 0 & 0 & 0 & 0 & 0 & 1 & 0\\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 1\end{pmatrix} \begin{pmatrix}a & b \\ 0 & 0 \\ 0 & 0 \\ a & b \\ c & d \\ 0 & 0 \\ 0 & 0 \\ c & d\end{pmatrix} = \begin{pmatrix}a & b \\\ c & d\end{pmatrix} $$Recall our discovery that:
$$ O_{L}\mid \phi^{+} \rangle = O_{R}^{T}\mid \phi^{+} \rangle$$where
$$O^{T} = \begin{pmatrix}a & c \\\ b & d\end{pmatrix} $$We can express this in diagrams:
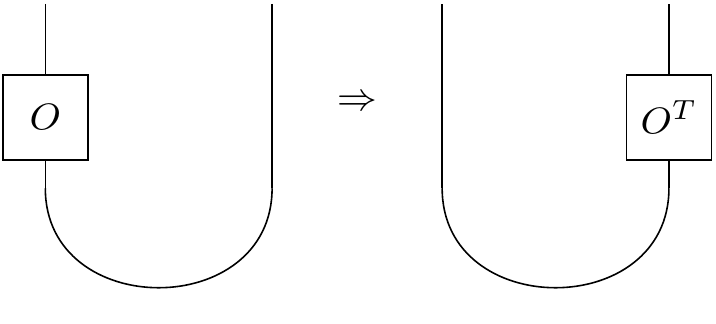
The idea is we can slide operators up and down wires and around cups and caps, which transpose them (just like in real life!).
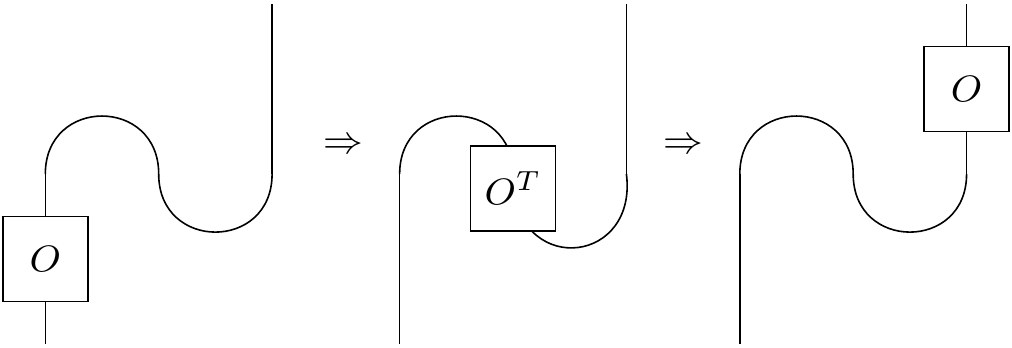
One useful thing to be able to do is take a partial trace. If we have two qubits A and B, we can trace over B to get the partial state of A, or trace over A to get the partial state of B. These partial states will be density matrices, a 2x2 Hermitian density matrix for A and B each. It's easy to see how to do this with the diagrams. First recall that a density matrix can be formed from a pure state vector by taking the outer product. In our case:
$ \rho_{A,B} = \mid\phi^{+}\rangle\langle\phi^{+}\mid $
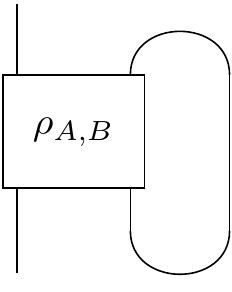
In other words, $ \rho_{A} = \big( I \otimes \cap \big) \big(\rho_{A,B} \otimes I \big) \big( I \otimes \cup \big) $.
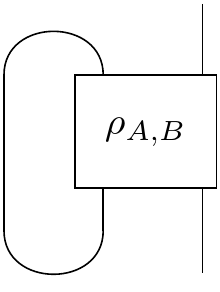
Aka: $ \rho_{B} = \big( \cap \otimes I \big) \big( I \otimes \rho_{A,B} \big) \big( \cup \otimes I \big) $.
On that note, the expectation value of an operator O on a density matrix $\rho$ is $tr(\rho O) $, where the trace is the sum along the diagonal of the matrix.
# Let's try it out in python.
import qutip as qt
import numpy as np
I = qt.identity(2)
cup = qt.Qobj(np.array([1,0,0,1]))
cup.dims = [[2,2], [1,1]]
cap = qt.Qobj(np.array([1,0,0,1])).dag()
cap.dims = [[1,1], [2,2]]
rhoAB = qt.bell_state("00")*qt.bell_state("00").dag()
rhoA = qt.tensor(I, cap)*qt.tensor(rhoAB, I)*qt.tensor(I, cup)
rhoB = qt.tensor(cap, I)*qt.tensor(I, rhoAB)*qt.tensor(cup, I)
# Compare with qutip's builtin function.
rhoA_ = rhoAB.ptrace(0)
rhoB_ = rhoAB.ptrace(1)
print(rhoA == rhoA_ and rhoB == rhoB_)