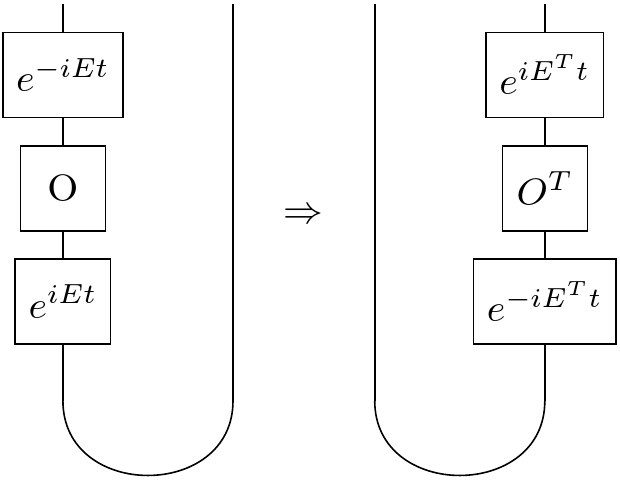
We return what you might call our original discovery.
$$ O_{L}\mid \phi^{+} \rangle = O_{R}^{T}\mid \phi^{+} \rangle$$An operator acting on the left side of the maximally entangled state $ \mid \phi^{+} \rangle $ is indistinguishable from the transpose of the same operator acting on the right side.
Let's consider an interesting case where we have a 2x2 energy operator E and:
$$ E_{L} = E \otimes I \\ E_{R} = I \otimes E^{T} $$We can consider the time evolved versions of our operator $ O $ on the left and right.
$$ O_{L} (t) = e^{iEt} O e^{-iEt} \otimes I $$$$ O_{R}^{T} (t) = I \otimes e^{iE^{T}t} O^{T} e^{-iE^{T}t} $$It follows that:
$$ O_{L} (-t) \mid \phi^{+} \rangle = O_{R}^{T} (t) \mid \phi^{+} \rangle$$The action of $ O $ on the left in the past (at -t) is equivalent to the action of $ O^{T} $ in the future (at t) on the right.
If we know the nice fact that $ (e^{-iEt})^{T} = e^{-iE^{T}t} $, this becomes obvious:
Let's consider a generalization of our setup.
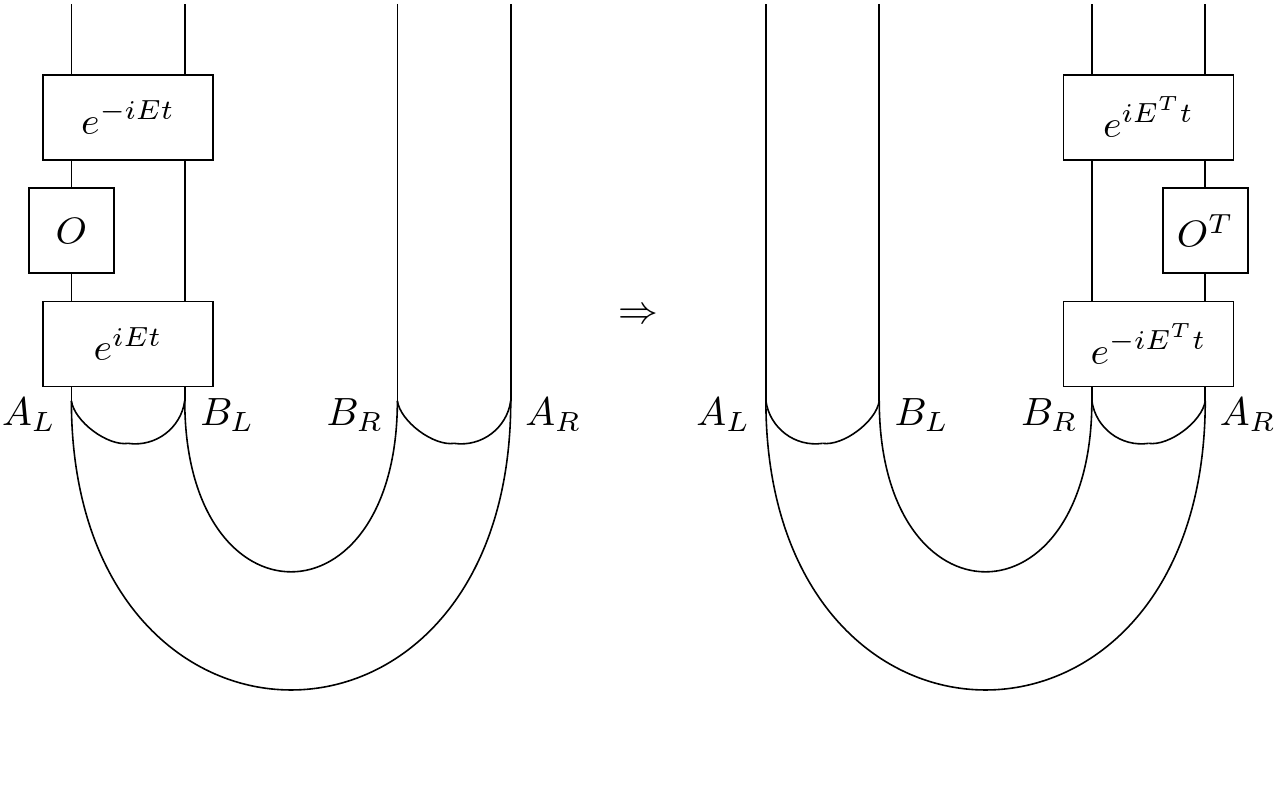
So we have four qubits. $A_{L}$ and $B_{L} $ on the left, and $B_{R}$ and $A_{R} $ on the right. The two sides left and right as a whole start off in a cup state. The generalization of the cup to any dimension is just:
$$ \mid\cup\rangle = \sum_{i, j}^{dim} \delta^{j}_{i} \mid i \rangle \mid j \rangle$$Here $ \delta^{j}_{i} = 1 $ if $ i = j $ else $ 0 $.
We've represented this multidimensional cup by a kind of tube because as you can see you can slide operators through it just as before. Given this we're then led to consider:
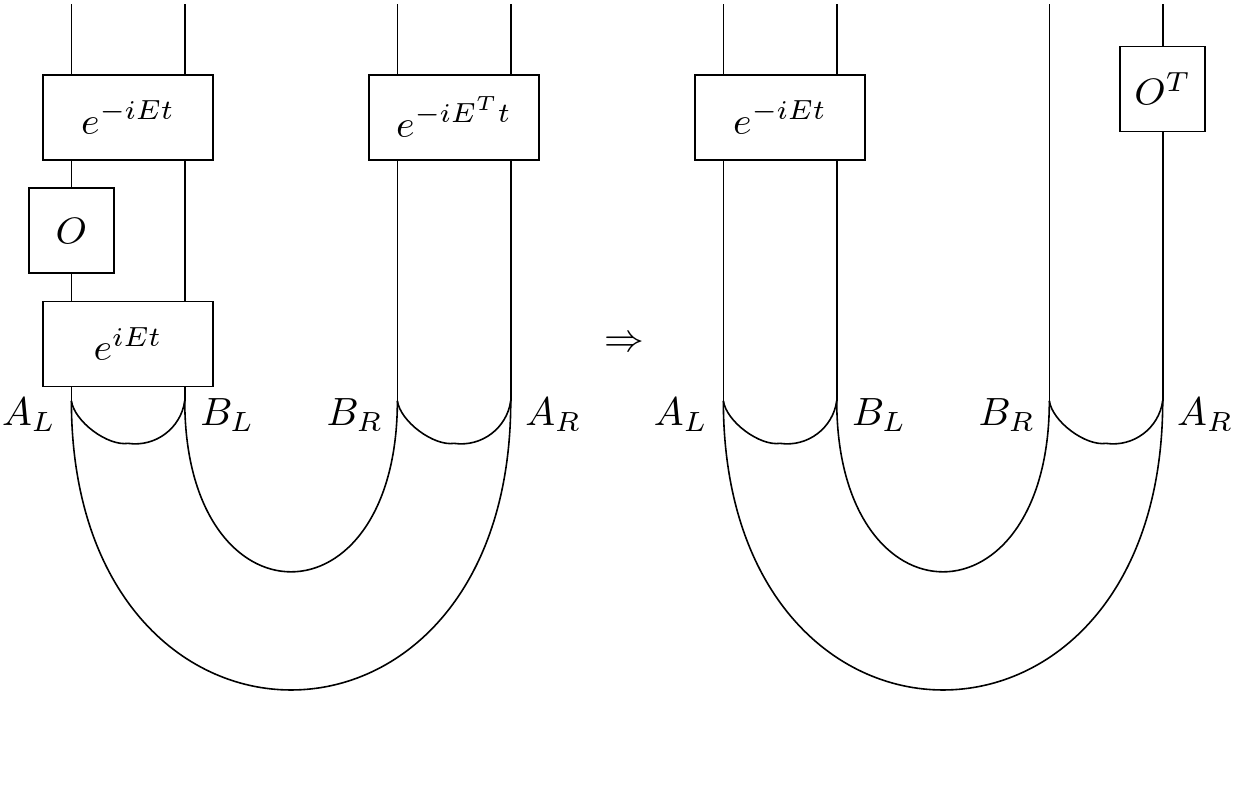
Continuing the theme of generalization, you're allowed to consider that $A_{L}, B_{L}, B_{R}, A_{R}$ actually contain any number of qubits as long as they match left and right. In our case, we'll consider the B's to have lots of qubits and the A's to have just one each.
Now one thing you might want to do is see if you can push a state through the tube like we can with an operator. Let's imagine swapping $A_{L}$ and $M$.
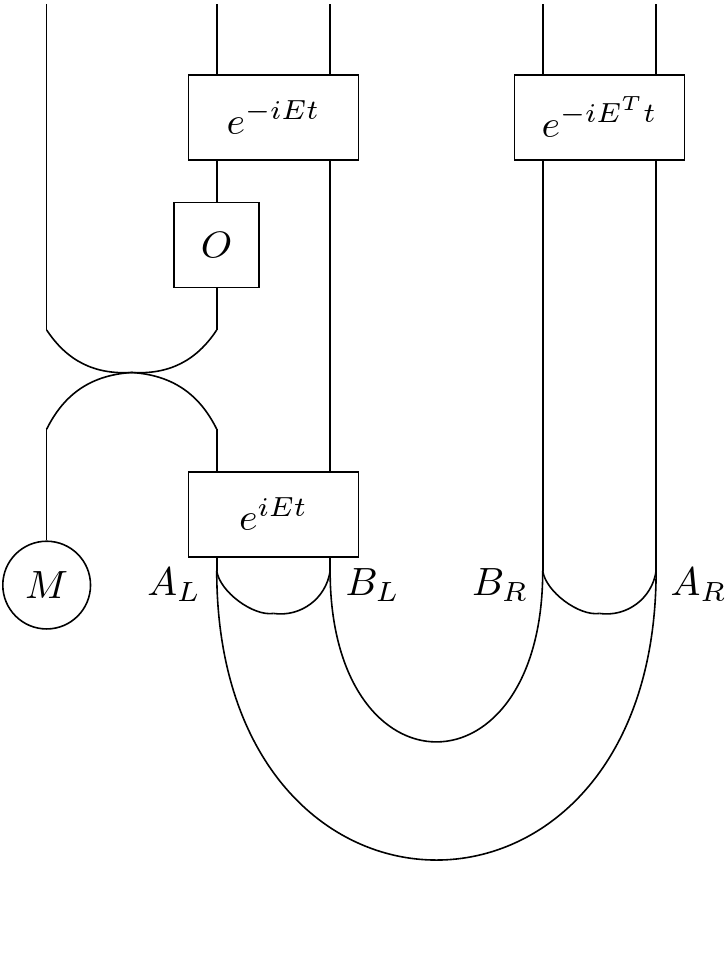
So far we don't have much of anything. Not only that but our operator O gets obstructed by the swap and can't slide down the tube anymore. Another generalization is: what if we consider a differen cup state? Specifically, let's consider a thermofield double or TFD state.
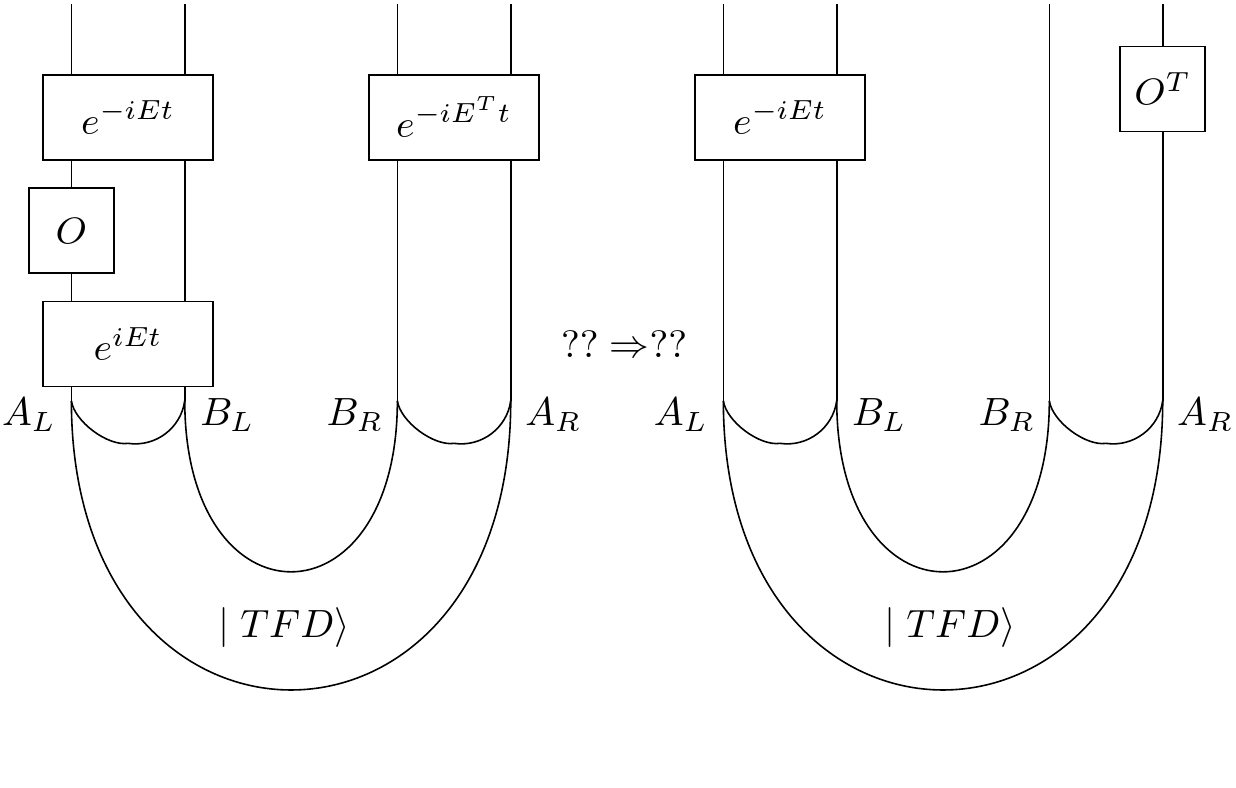
But what is the thermofield double state?
$$ \mid TFD \rangle = \frac{1}{tr(e^{-\beta E})} \sum_{j} e^{-\frac{1}{2} \beta E_{j}} \bar{\mid E_{j} \rangle} \mid E_{j} \rangle $$The overline above $ \bar{\mid E_{j} \rangle} $ denotes complex conjugation, and $\beta = \frac{1}{T} $ where $T$ is the temperature. So as $ \beta \to 0, T \to \infty $. In the limit of infinite temperature, $ \mid TFD \rangle = \mid \cup \rangle $, which reduces to the case considered before. At lower temperatures, however, we get a different entangled state. The point is that the two sides of the TFD are entangled in terms of their energy basis.
It has been hypothesized that the TFD state is a good model of two entangled black holes aka a double sided black hole.
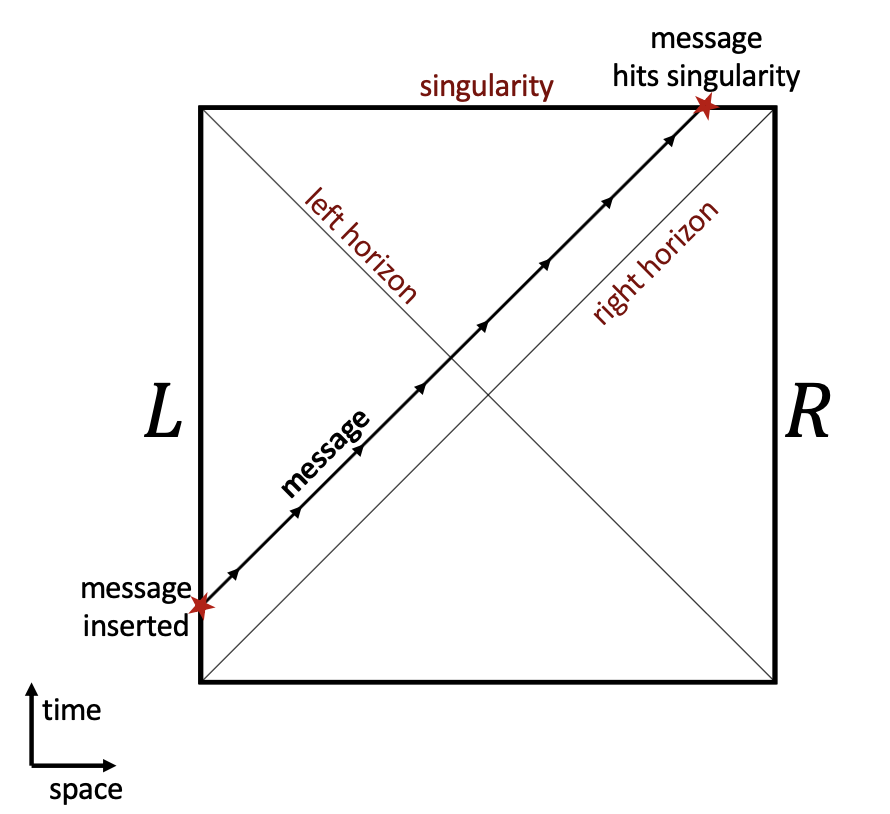
The above is a spacetime diagram of the situation. We have our left half and our right half and they're entangled in the TFD state. We're imagining things traveling at the speed of light, which here is a path at 45 degrees. We act with our operator $ O $ in the past ("message inserted") on the left black hole. It goes off, passes the left event horizon (from which there is no return, as the pull of gravity is so strong not even light can escape) and continues on until it hits the "singularity" and then it's lights out. This is just like the case we've been considering where because we're using a finite temperature TFD state or because we're swapping a message state in instead of acting with an operator--or both! In any case, there's an obstruction and so our business on the left can't go through the tube and come out on the right.
What if I told you there's an "easy" way of fixing our problem? After all, we were able to get things to teleport from place to place by making a measurement and then a correction, or by coupling the two sides. Let's do something similar here. In spacetime terms, we're going to get this diagram:
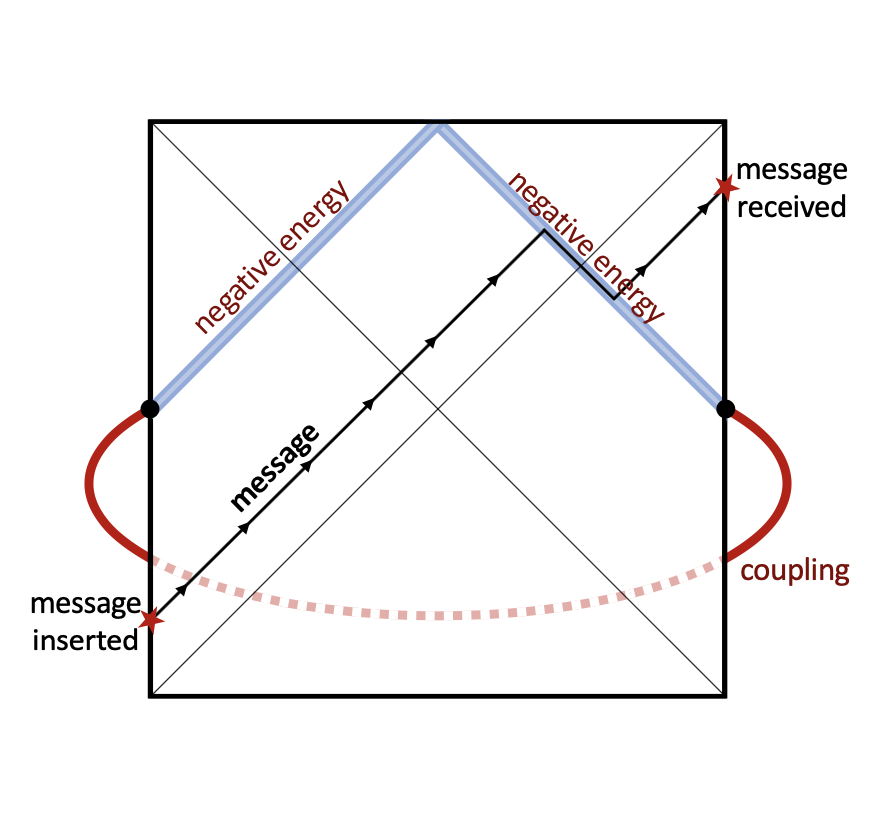
We insert our message. And then at a later time couple the left side and right side "from outside." In geometrical terms, this corresponds to a negative energy shockwave that propagates to the singularity. But if things hit a negative energy shockwave, they are translated back in time. So when our message hits the negative coupling, it's translated in such a way that it ends up beyond the event horizon on the right side! So it emerges and we can receive it on the right. In the string diagrams:
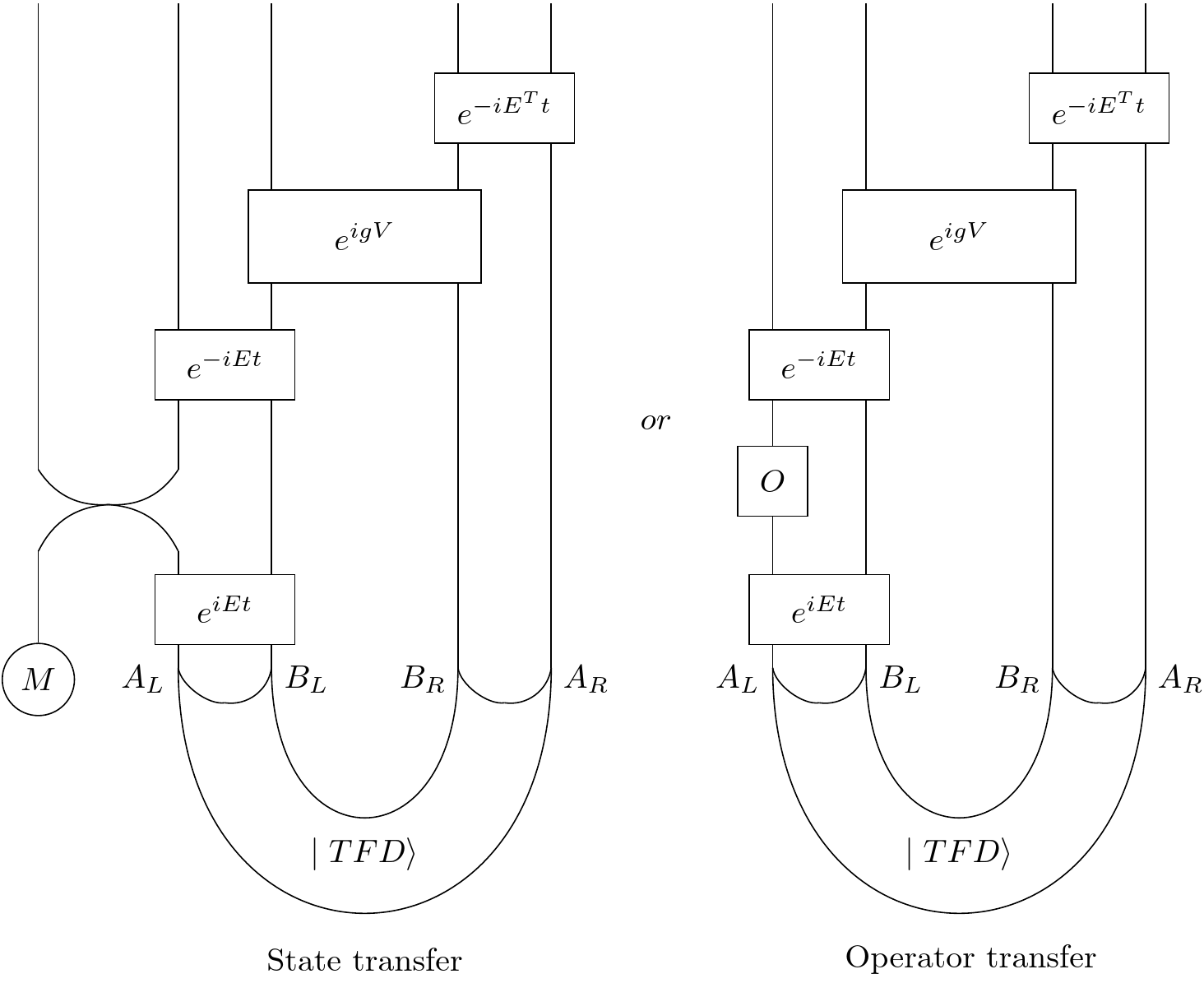
So we already know operator transfer can work at infinite temperature without a coupling but let's consider these more general case. What's interesting is that our coupling $ e^{igV} $ acts only on the B's, and yet we shall see it can get the job done: the operator (or state) inserted in the past on the left will remerge in the future on the right. So in what circumstances will this work?
First, we shall see that a good choice of $ V $ is:
$$ V = \frac{1}{b-a} \sum_{i}^{b} Z_{i, L} Z_{b-i, R} $$So $b$ is the number of B qubits (in $B_{L}$ or $B_{R}$) and $a$ is the number of A qubits (in $A_{L}$ or $A_{R}$). We iterate over the B qubits and for each pair of B's (one of the left, one on the right) we multiply their Z operators (acting only on $B_{i, L}$ and $B_{i, R}$) and sum it all up.
Abusing our diagram language, we could represent this like:
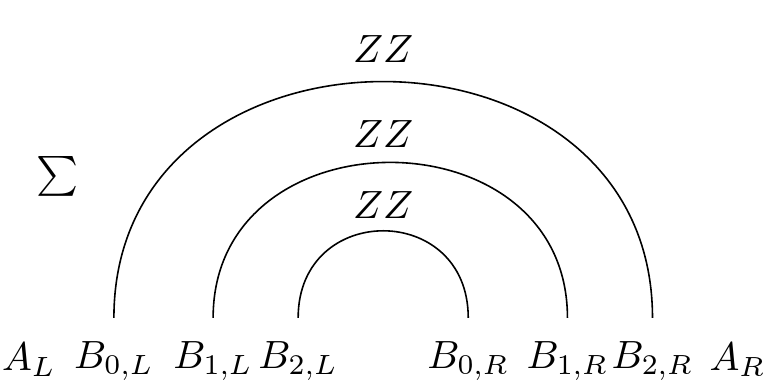
There of course remains the question of the parameter $ g $ which we shall return to. But first let's play around with the TFD a bit.
If we start with the TFD state at temperature $ \frac{1}{\beta} $ and take the partial trace on either side we get the same state $\rho_{\beta} $ on the left and the right. We consider the square root of $\rho_{\beta} $, $\rho_{\beta}^{\frac{1}{2}} $, such that $ \rho_{\beta}^{\frac{1}{2}} \rho_{\beta}^{\frac{1}{2}} = \rho_{\beta} $. It turns out we can calculate it directly:
$$ \rho_{\beta}^{\frac{1}{2}} = \frac{e^{-\frac{1}{2}\beta E}}{tr(e^{-\frac{1}{2}\beta E})}$$And actually we can go in the reverse direction and use $ \rho_{\beta}^{\frac{1}{2}} $ to prepare the TFD state from the cup state. The TFD state is just $ \rho_{\beta}^{\frac{1}{2}} $ strung out as a vector! (In passing I mention that it's always difficult to keep track of the normalization of these things.)
$$ I \otimes \rho_{\beta}^{\frac{1}{2}}\mid\cup\rangle \ = \rho_{\beta}^{\frac{1}{2}} \otimes I \mid\cup\rangle \ = \ \mid TFD \rangle $$So let's think back from before. We had:
$$ O_{L} (-t) \mid \cup \rangle = O_{R}^{T} \mid \cup \rangle $$We now want to consider:
$$ O_{L} (-t) \mid TFD \rangle $$But that's just:
$$ O_{L} (-t) \mid TFD \rangle \to O_{L} (-t) \rho_{\beta, R}^{\frac{1}{2}} \mid \cup \rangle $$We've chosen to act with $ \rho $ on the right. Why? Because it means that $O_{L} (-t)$ and $ \rho_{\beta, R}^{\frac{1}{2}} $ must commute since one acts on the left and the other acts on the right. So we can do a little switcheroo:
$$ O_{L} (-t) \mid TFD \rangle \to \rho_{\beta, R}^{\frac{1}{2}} O_{L} (-t) \mid \cup \rangle $$But that latter is just:
$$ O_{L} (-t) \mid TFD \rangle \to \rho_{\beta, R}^{\frac{1}{2}} O_{R}^{T} (t) \mid \cup \rangle $$Similarly, just from the definition of the TFD, we have on the other side:
$$ O_{R}^{T} (t) \mid TFD \rangle \to O_{R}^{T} (t) \rho_{\beta, R}^{\frac{1}{2}} \mid \cup \rangle $$In other words, the only difference between $ O_{L} (-t) \mid TFD \rangle $ and $ O_{R}^{T} (t) \mid TFD \rangle $ is the order of the factors: $ \rho_{\beta, R}^{\frac{1}{2}} O_{R}^{T} (t) $ vs $ O_{R}^{T} (t) \rho_{\beta, R}^{\frac{1}{2}} $ that act on the cup. In other words, the difference between the two operators is that one is the adjoint of the other $ \big( \rho_{\beta, R}^{\frac{1}{2}} O_{R}^{T} (t) \big)^{\dagger} = O_{R}^{T} (t) \rho_{\beta, R}^{\frac{1}{2}} $.
We've clearly got something going on. But whether this construction will pay dividends depends on our choice of energy operator $ E $...