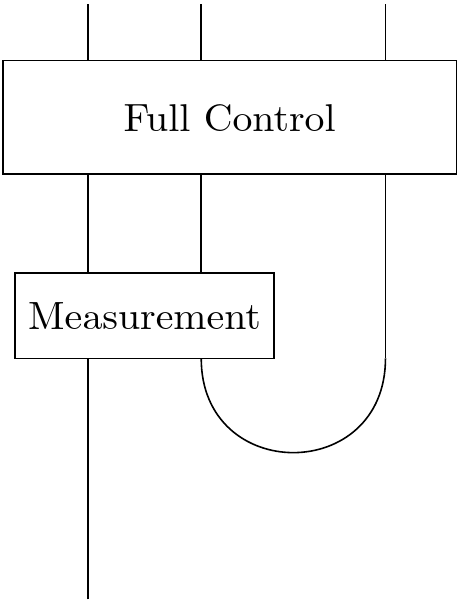
Let's generalize the yanking equation into the algorithm for quantum teleportation. So we start off with a qubit A and a cup, which we can think of as two entangled qubits B and C. And someone takes C very far away, and we're left with A and B. We're going to teleport A to C.
So A is some $a\mid\uparrow\rangle + b\mid\downarrow\rangle $, we start out in the state $\mid A \rangle \otimes \mid\cup\rangle $.
First, we shatter the perfect symmetry of the yanking equation by making a measurement on A and B. Specifically, we make a measurement in the "Bell basis".
$$ \mid\Phi^{+}\rangle = \ \mid\uparrow\uparrow\rangle \ + \mid\downarrow\downarrow\rangle \\ \mid\Phi^{-}\rangle = \ \mid\uparrow\uparrow\rangle \ - \mid\downarrow\downarrow\rangle \\ \mid\Psi^{+}\rangle = \ \mid\uparrow\downarrow\rangle \ + \mid\downarrow\uparrow\rangle \\ \mid\Psi^{-}\rangle = \ \mid\uparrow\downarrow\rangle \ - \mid\downarrow\uparrow\rangle $$These four vectors form a complete basis for all two qubit states. (Indeed, the first is quite familiar to us!) We can find the probabilities of each of the outcomes on A and B using the corresponding projectors. (Incidentally, there should be factors of $ \frac{1}{\sqrt{2}} $ everywhere for the probabilities to work out.) Nature chooses one of the four at random given those probabilities, and we apply the projector corresponding to that outcome. So after the measurement, A and B are in one of those four states, and we've gotten an outcome: 1, 2, 3, or 4. This choice can be described with two bits: 00 01 10 11: hence, the two black nodes.
Let's work it out explicitly in the case of outcome 1.
$$ \mid A \rangle \otimes \mid\Phi^{+}\rangle = \big( \begin{pmatrix}a \\\ b \end{pmatrix} \otimes \begin{pmatrix}1 \\\ 0 \\\ 0 \\\ 1 \end{pmatrix} \big) = \begin{pmatrix}a \\\ 0 \\\ 0 \\\ a \\\ b \\\ 0 \\\ 0 \\\ b \end{pmatrix}$$$$ \big( \mid\Phi^{+}\rangle \otimes \langle\Phi^{+}\mid \big) \otimes I \ = \big( \begin{pmatrix}1 & 0 & 0 & 1 \end{pmatrix} \otimes \begin{pmatrix}1 \\\ 0 \\\ 0 \\\ 1 \end{pmatrix} \big) \otimes \begin{pmatrix}1 & 0 \\\ 0 & 1 \end{pmatrix} = \\ \begin{pmatrix}1 & 0 & 0 & 1 \\\ 0 & 0 & 0 & 0 \\\ 0 & 0 & 0 & 0 \\\ 1 & 0 & 0 & 1 \end{pmatrix} \otimes \begin{pmatrix}1 & 0 \\\ 0 & 1 \end{pmatrix} = \begin{pmatrix} 1 & 0 & 0 & 0 & 0 & 0 & 1 & 0\\\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 1\\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\\ 1 & 0 & 0 & 0 & 0 & 0 & 1 & 0\\\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 1 \end{pmatrix} $$$$ \big( \big( \mid\Phi^{+}\rangle \otimes \langle\Phi^{+}\mid \big) \otimes I \big) \big( \mid A \rangle \otimes \mid\Phi^{+}\rangle \big) = \begin{pmatrix} 1 & 0 & 0 & 0 & 0 & 0 & 1 & 0\\\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 1\\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\\ 1 & 0 & 0 & 0 & 0 & 0 & 1 & 0\\\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 1 \end{pmatrix}\begin{pmatrix}a \\\ 0 \\\ 0 \\\ a \\\ b \\\ 0 \\\ 0 \\\ b \end{pmatrix} = \begin{pmatrix}a \\\ b \\\ 0 \\\ 0 \\\ 0 \\\ 0 \\\ a \\\ b \end{pmatrix} $$We observe that: $$ \begin{pmatrix}1 \\\ 0 \\\ 0 \\\ 1\end{pmatrix} \otimes \begin{pmatrix}a \\\ b \end{pmatrix} = \begin{pmatrix}a \\\ b \\\ 0 \\\ 0 \\\ 0 \\\ 0 \\\ a \\\ b\end{pmatrix} $$
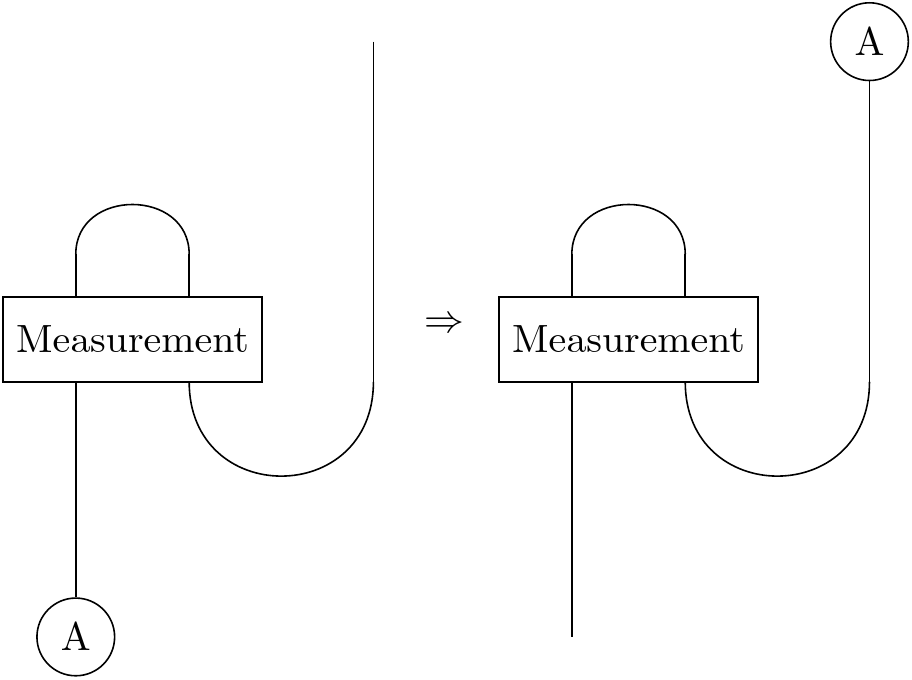
The teleportation was successful! A swapped places with C.
If we do the same calculation for each of the four outcomes, we end up in one of these four states:
$$ \big(\mid\Phi^{+}\rangle \langle \Phi^{+} \mid \otimes I \big) \big( \mid A \rangle \otimes \cup \big) = \ \mid\Phi^{+}\rangle \otimes \begin{pmatrix}a \\ b\end{pmatrix} $$$$ \big(\mid\Phi^{-}\rangle \langle \Phi^{-} \mid \otimes I \big) \big( \mid A \rangle \otimes \cup \big) = \ \mid\Phi^{-}\rangle \otimes \begin{pmatrix}a \\ -b\end{pmatrix} $$$$ \big(\mid\Psi^{+}\rangle \langle \Psi^{+} \mid \otimes I \big) \big( \mid A \rangle \otimes \cup \big) = \ \mid\Psi^{+}\rangle \otimes \begin{pmatrix}b \\ a\end{pmatrix} $$$$ \big(\mid\Psi^{-}\rangle \langle \Psi^{-} \mid \otimes I \big) \big( \mid A \rangle \otimes \cup \big) = \ \mid\Psi^{-}\rangle \otimes \begin{pmatrix}-b \\ a\end{pmatrix} $$So we can see that if we measure in the Bell basis, then the qubit C ends up identical to A, up to some swaps and sign flips. We can reason like this: Entanglement is monogamous. So if B and C were maximally entangled, but now A and B are projected into the maximally entangled state, then C is forced to be whatever A was.
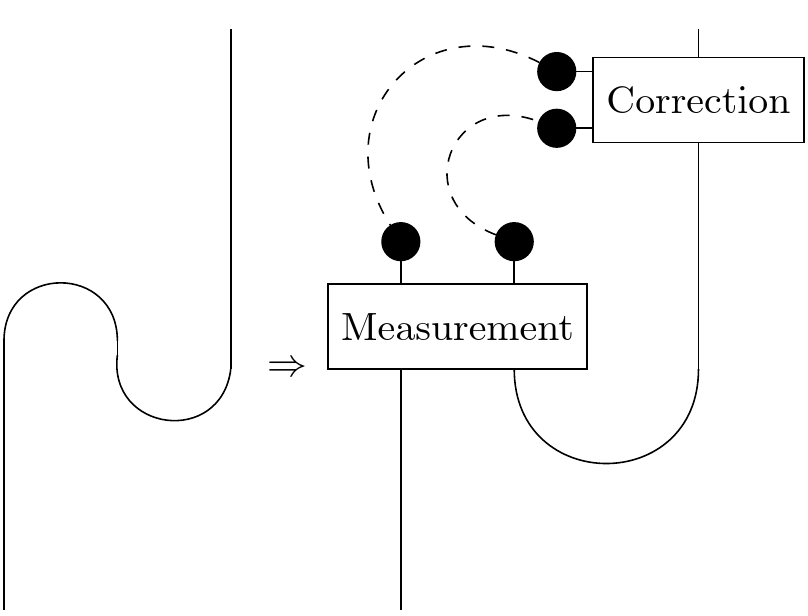
The dotted lines represent classical communication. We can use our knowledge of the outcome of the measurement to correct for the swaps and sign flips. In some way or other, we communicate our two bits to our faraway friend who has qubit C. Naturally, we can't send such a signal faster than the speed of light.
If we sent "1", then our friend doesn't have to do anything! In fact, in that case, the teleportation diagram reduces down to our old friend the yanking equation.
The full set of rules is:
$$ \begin{matrix} 1 & \to & I \\\ 2 & \to & Z \\\ 3 & \to & X \\\ 4 & \to & ZX \end{matrix} $$where X and Z refer to the Pauli matrices:
$$ X = \begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix} Y = \begin{pmatrix} 0 & -i \\ i & 0 \end{pmatrix} Z = \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix} $$In other words, if we'd sent "2", our friend would apply the Z operator to C which flips the sign of the second component. If we'd sent "3", our friend would apply the X operator which swaps the two components. And if we'd sent "4", our friend would apply X to swap the components, and then Z to flip the sign of the second. And then the teleportation would be complete.
Two things make this more powerful than classical communication alone: a) although we've sent two classical bits, we've teleported an unknown quantum state b) if A had been entangled with some other qubits, then the A that would emerge at C would have all the same entanglement, which picks it out uniquely as itself and not some kind of forgery.
It's worth noting that there's an alternative formulation of quantum teleportation where you make two Z measurements on A and B instead of measuring them both in the Bell basis. (If a box has the black nodes coming out of it, that means measure that operator, not apply that operator.)
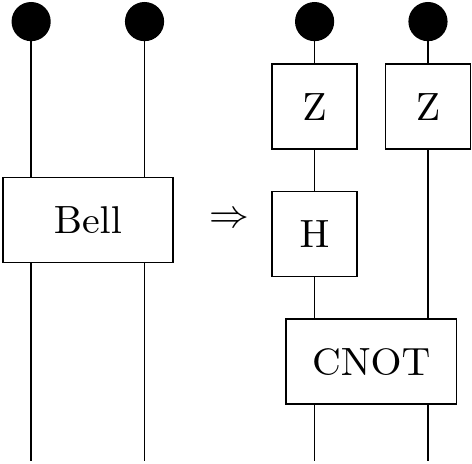
$CNOT = \begin{pmatrix} 1 & 0 & 0 & 0 \\\ 0 & 1 & 0 & 0 \\\ 0 & 0 & 0 & 1 \\\ 0 & 0 & 1 & 0 \end{pmatrix} $
The idea of a $CNOT$ operator is that it acts on two qubits A and B, and if A = $\mid\uparrow\rangle $, then B remains the same; but if A = $\mid\downarrow\rangle$, then it flips B (aka applies the X operator). A is the "control" and B is the "target."
$H = \frac{1}{\sqrt{2}}\begin{pmatrix} 1 & 1 \\\ 1 & -1 \end{pmatrix} $
H is the "Hadamard" operator. It sends:
$$ \mid\uparrow\rangle \to \frac{\mid\uparrow\rangle \ + \mid\downarrow\rangle}{\sqrt{2}}$$$$ \mid\downarrow\rangle \to \frac{\mid\uparrow\rangle \ - \mid\downarrow\rangle}{\sqrt{2}}$$In fact, it sends eigenstates of the Z operator to eigenstates of the X operator--it's actually the 2x2 Fourier transform operator. (Indeed, Z generates translations in X-space; and X generates translations in Z-space: as one can confirm by rotating a sphere around the Z axis from X+ and X- and back; or around the X axis between Z+ and Z- and back.)
Finally, we make Z measurements on A and B and get: $ \uparrow\uparrow $, $ \uparrow\downarrow $, $ \downarrow\uparrow $, or $ \downarrow\downarrow $: we send those two bits to our friend with C, and interestingly, the same corrections are applied.
One could imagine taking the classical communication out of the picture.
After our measurement, we could apply a quantum operator to A, B, and C. It would be a controlled operator like $CNOT$, and apply the correction on C depending on the state of A and B. We could construct it like this:
$$ \mid 1, \uparrow \rangle \ \langle 1, \uparrow \mid + \mid 1, \downarrow \rangle \ \langle 1, \downarrow \mid + \mid 2, Z\uparrow \rangle \ \langle 2, \uparrow \mid + \mid 2, Z\downarrow \rangle \ \langle 2, \downarrow \mid + \\ \mid 3, X\uparrow \rangle \ \langle 3, \uparrow \mid + \mid 3, X\downarrow \rangle \ \langle 3, \downarrow \mid + \mid 4, ZX\uparrow \rangle \ \langle 4, \uparrow \mid + \mid 4, ZX\downarrow \rangle \ \langle 4, \downarrow \mid $$