(A Little) More on Quantum Reference Frames¶
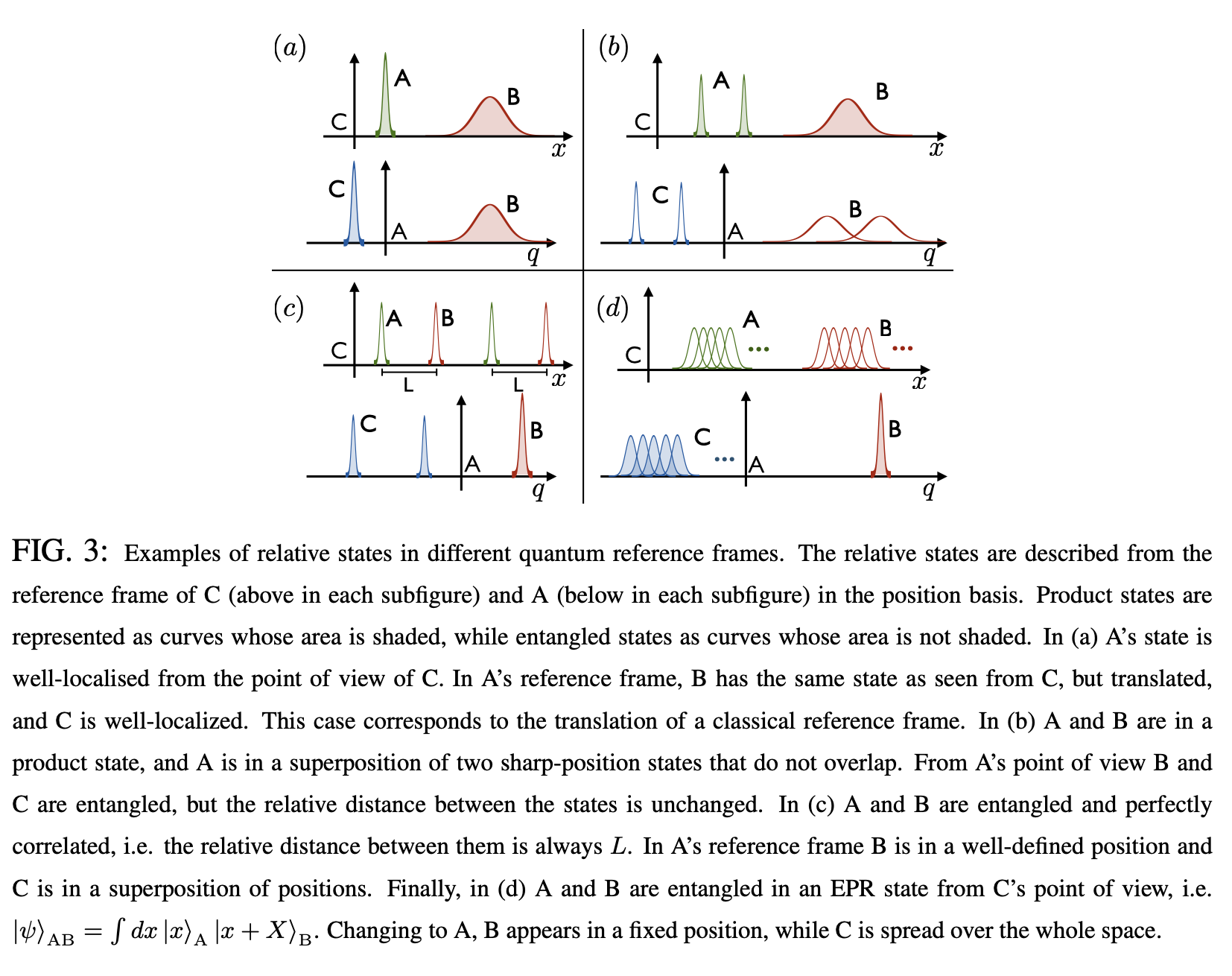
Following Giacomini, Castro-Ruiz and Brukner (as well as others including Galley and de la Hamette), the basic principle here is that of a "coherent change of reference frame." Above, we see an example in terms of position, but the notion can be generalized for other observables related to other symmetry groups.
We have three systems $A, B,$ and $C$. In (a), $C$ is regarded as the reference, and so by definition, it's at the origin and in a separable state. From $C$'s point of view, $A$ and $B$ are wavepackets located to the right. If instead we take $A$'s perspective, $A$ would be regarded as the origin, and $C$ would be to its left and $B$ would be to its right. This is no different from a classical change of reference frame.
The interesting case, however, is: what if $A$ is in a superposition of two wavepackets, and we want to jump from $C$'s perspective to $A$'s perspective? Since $C$ regards $A$ and $B$ as being in (basically) two locations each, $A$ conversely would regard $C$ and $B$ as being in two locations, and moreover in an entangled state, so that the two possible locations for $B$ and $C$ are correlated.
In other words, the supposition being made in this kind of work is that entanglement and superposition are entirely reference frame dependent. If a quantum system is chosen as a reference, what that means is that it's regarded as the "origin," as separable, in the "0" state, no entanglement, no superposition, nothing. If from another perspective, that system had been entangled and in superposition, that "quantumness" is precisely externalized to the systems coordinatized relative to the reference.
We could think in terms of spins: suppose $A$ is regarded as the reference, and therefore it's always just in the $\mid \uparrow \rangle$ state (or any other arbitrarily chosen state), and suppose $B$ and $C$ are in the $\mid \uparrow \uparrow \rangle + \mid \downarrow \downarrow \rangle$ state. If we switch to $B$'s reference frame, then now $B$ must be regarded as in the $\mid \uparrow \rangle$ state. Since $B$ and $C$ were in the entangled state $\mid \uparrow \uparrow \rangle + \mid \downarrow \downarrow \rangle$ relative to $A$, then $C$ must agree with $B$, and since $B$ is $\uparrow$, so $C$ must be be $\uparrow$. So $B$ and $C$ are in the $\mid \uparrow \uparrow \rangle$ state. But what about $A$'s state relative to $B$? From $A$'s perspective it was 50/50 whether $B$ (and $C$) were going to be $\uparrow$ or $\downarrow$, and so if now we regard $B$ (and $C$) to be $\uparrow$, then $A$ must be in the state $\mid \uparrow \rangle + \mid \downarrow \rangle$.
Lest this seem ad hoc, this procedure can be formalized as a certain unitary transformation. The argument of course depends on these systems all having essentially the same Hilbert space, with states being representations of the same symmetry group, and it's an interesting question how to fully generalize the idea when the reference system has many different kinds of systems associated with it. In the general case, it's possible the transformations won't necessarily by unitary.
Incidentally, this formulation of QRF's relates quantum states, each explitly from a "point of view," to each other, but the whole construction can be placed in a reference frame independent context. In other words, one can consider Dirac-type quantization, where one imagines, that for example, the overall momentum of all particles (say 3 particles) must be $0$ insofar as there is no external reference frame to distinguish anything other than that. Then one can posit that one of the particles is "standing still at the origin," and describe the quantum state of the other particles with reference to that particle.
The code below implements the "coherent change of reference" operator, given a state from some perspective, a subsystem index specifying the perspective to which to switch, a function $G(i)$ which takes basis state indices as input and returns the group element that prepares that basis state from a reference basis state, and a list of basis states (computational basis by default).
In the case of systems on a discrete circle, $G(i)$ is just $T^{i}$ where $T$ is the shift operator, while for qubits with $Z+$ as a reference state, $G(i)$ is $I$ if $i=0$ and $X$ if $i=1$.
The basic idea: If we want to switch from POV $a$ to POV $b$, for each basis state $\mid i \rangle$, we form the operator:
$$O_{i} = I_{a} \otimes [G(i)^{\dagger}\mid 0 \rangle\langle i \mid]_{b} \otimes [G(i)^{\dagger}]^{\otimes rest} $$We then add up all these operators, and swap $a$ and $b$: $U_{a\rightarrow b} = SWAP_{a,b}\sum_{i} O_{i}$. The effect is to push $b$ into the reference basis state, while dragging everybody else along with it. It implements the basic principle of "coherent change of reference":
If $\mid \psi \rangle^{a} \rightarrow \mid \psi \rangle^{b}$ and $\mid \phi \rangle^{a} \rightarrow \mid \phi \rangle^{b}$, then $(\alpha \mid \psi \rangle + \beta \mid \phi \rangle)^{a} \rightarrow (\alpha \mid \psi \rangle + \beta \mid \phi \rangle)^{b}$.
import numpy as np
import qutip as qt
from itertools import permutations, product
def construct_swap(a, b, dims):
perm = list(range(len(dims)))
perm[a], perm[b] = perm[b], perm[a]
tensor_indices = list(product(*[[(i, j) for j in range(dims[i])] for i in range(len(perm))]))
ptensor_indices = list(product(*[[(i, j) for j in range(dims[i])] for i in perm]))
m = np.zeros((len(tensor_indices), len(tensor_indices)))
for i, pind in enumerate(ptensor_indices):
m[i, [tensor_indices.index(p) for p in permutations(pind) if p in tensor_indices][0]] = 1
M = qt.Qobj(m)
M.dims = [dims, dims]
return M
def take_pov(state, from_pov, to_pov, G, basis=None, return_map=False):
if from_pov == to_pov:
return state
n = len(state.dims[0])
d = state.dims[0][0]
basis = basis if type(basis) != type(None) else [qt.basis(d, i) for i in range(d)]
g_inv = lambda i: G(i).dag()*basis[0]
O = construct_swap(from_pov, to_pov, state.dims[0])*\
sum([qt.tensor(*[qt.identity(d) if j == from_pov \
else g_inv(i)*basis[i].dag() if j == to_pov \
else G(i).dag() for j in range(n)]) for i in range(d)])
return O if return_map else O*state
Check out ring_qrf.py for a visualization of QRF shifts in the case of discrete quantum systems on a circle, and qbit_qrf.py for a qubit based example!